
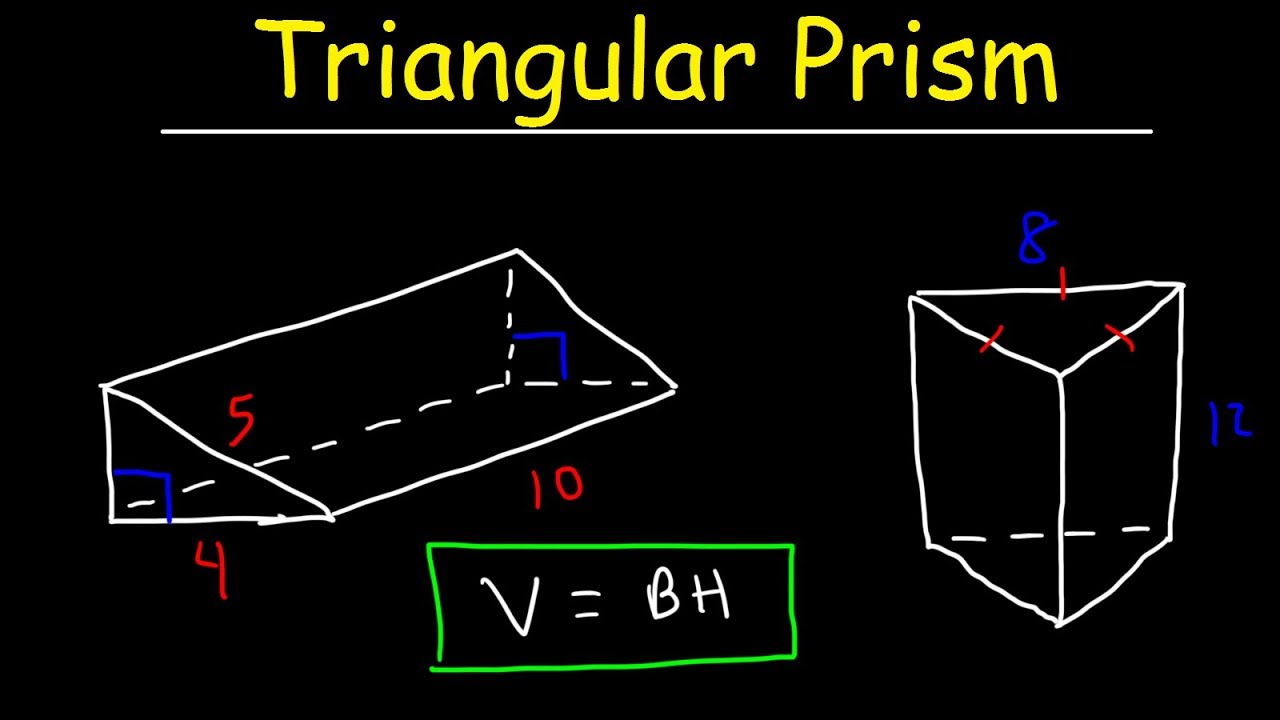
Here are some examples of finding the volume of a prism using the formula: Example 1įind the volume of a rectangular prism with a base of length 5 cm and width 8 cm, and a height of 10 cm.įind the volume of a triangular prism with a base of height 4 cm and base width 6 cm, and a height of 12 cm. The calculator will automatically calculate the volume of the prism. The formula to calculate the volume for prisms is always the same: Volume prism Area base Length In this case, the area of the base of the prism is the Solve equation To solve an equation, one must find the value of the variable that makes the equation true.Enter the area of the base of the prism.Our prism volume calculator is designed to make it easy for you to find the volume of any prism.
Where V is the volume, S is the area of the base, and h is the height of the prism. The volume of an isosceles right angled triangular prism is Right angle prism by Steve Ladbrook - JHow to calculate the volume of a right angle prism. The formula for finding the volume of a prism is: Whether you are a student, a teacher, or someone who needs to work with prisms, our prism volume calculator can help you find the volume of any prism with ease. The dual of a right n-prism is a right n- bipyramid.Ī right prism (with rectangular sides) with regular n-gon bases has Schläfli symbol, two parallel line segments, connected by two line segment sides.Calculating the volume of a prism is an essential skill in geometry. This applies if and only if all the joining faces are rectangular. Oblique vs right Īn oblique prism is a prism in which the joining edges and faces are not perpendicular to the base faces.Įxample: a parallelepiped is an oblique prism whose base is a parallelogram, or equivalently a polyhedron with six parallelogram faces.Ī right prism is a prism in which the joining edges and faces are perpendicular to the base faces. However, this definition has been criticized for not being specific enough in relation to the nature of the bases, which caused confusion among later geometry writers. Euclid defined the term in Book XI as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. Step 2: Find the volume of the prism by plugging the values found in step 1 into the formula for the volume of a triangular.
#FIND THE VOLUME OF TRIANGULAR PRISM HOW TO#
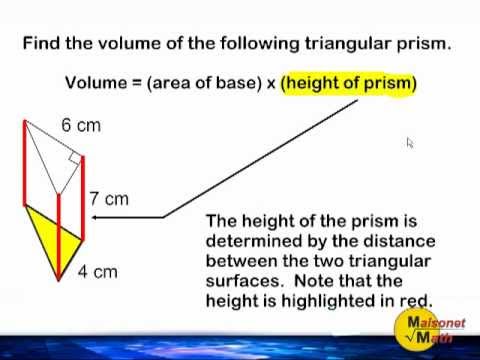
Like many basic geometric terms, the word prism (from Greek πρίσμα (prisma) 'something sawed') was first used in Euclid's Elements. Step 1: Identify the given dimensions of the triangular prism. How to Find the Volume of a Triangular Prism Math with Mr. a prism with a pentagonal base is called a pentagonal prism. All cross-sections parallel to the bases are translations of the bases. In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy (rigidly moved without rotation) of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases.

Uniform in the sense of semiregular polyhedronĬonvex, regular polygon faces, isogonal, translated bases, sides ⊥ basesĮxample: net of uniform enneagonal prism ( n = 9) Example: uniform hexagonal prism ( n = 6) Any prism volume is V BH where B is area of base and H is height of prism, so find area of the base by B 1/2 h (b1+b2), then multiply by the height of the prism.


 0 kommentar(er)
0 kommentar(er)
